
Osoba nieznająca statystyki widząc wyniki kolejnego sondażu zada czasem pytanie: czy i jak opinia przebadanych 1000 osób może być podstawą do formułowania wniosku o poglądach wielomilionowej populacji? Na ile wiarygodna jest ta informacja, czy można jej wierzyć?
Odpowiedź brzmi i tak i nie. Tak, bo niesie ona wiedzę i nie, bo ta wiedza jest z natury rzeczy niepewna. Sondaż jest bowiem bardzo niedoskonałą fotografią i to raczej wykonaną Camera obscura w śreżodze (takie rozgrzane powietrze nad asfaltem, ponoć słowo nieznane). Ale ta fotografia mówi już całkiem sporo.
Wpis dzisiejszy dotyczyć będzie TYLKO i WYŁĄCZNIE kwestii tzw. błędu losowego (patrz niżej). Milcząco więc zakładamy na czas czytania, że:
- pytania były poprawnie sformułowane i zadane w odpowiedniej kolejności,
- każdy zapytany udzielił odpowiedzi,
- każdy obywatel udzielił prawdziwej odpowiedzi,
- …
i tak by można ciągnąć tę listę naprawdę dłuuuuuuuuuugo (ale to temat na inną notkę).
Błąd losowy jest błędem wynikającym z faktu, że pytana jest nie cała a tylko część populacji. Losując próbę często dostaniemy taką, która jest dobrą fotografią populacji, ale też trafią się i takie, które będą fotografią populacji w baaaaardzo krzywym lustrze.
Zacznijmy więc od … no tak, znowu te monety, które mają idealny kształt i w 50% przypadków dają orła (w rzeczywistości monety wcale tak idealne nie są, a i na kant mogą upaść, ale to już insza inszość). Co się zatem by stało, gdybyśmy wielokrotnie rzucali na raz 100 monet? Ile orłów i jak często by wypadało? Odpowiedź na rysunku, proszę zerknąć na słupki, im wyższy, tym większa szansa na wynik podany pod słupkiem:

I tak średnio w 80 przypadkach na 1000 dostalibyśmy dokładnie 50 orłów, czyli wynik „prawdziwy”. W 78 przypadkach na 1000 mielibyśmy malutki „błąd”, bo nie 50 a 49 lub 51 i tak dalej. Za każdym razem szansa na coraz większy „błędny” wynik maleje.
Gdybyśmy te wyniki zsumowali to 96,5% przypadków wynik będzie w granicach 40-60 orłów, a wyniki które pominięto na wykresie mają szansę wystąpić 2 razy na 1000.
Dokładnie tak też jest z sondażami. Przyjmijmy, że w populacji dokładnie połowę stanowią osoby tej lepszej płci. Szansa na to, że na 1000 osób wylosowanych zostanie mniej niż 464 (K/M – skreślić zgodnie z własnymi poglądami) wynosi 1% a mniej niż 452 już tylko 0,1%. Szanse na to, że w próbie znajdzie się mniej niż 400 osób lepszej płci są iluzoryczne, ponad 500 razy łatwiej jest bowiem trafić 6 w totka.
Dostając zatem sondaż, w którym dana partia ma np. 25% (naukowo nazywa się to oszacowaniem punktowym) wiem, że owszem jest to w tym momencie najbardziej prawdopodobny wynik który znam. Ale wiem też, że są dość duże szanse na to, że wynik jest trochę mniejszy lub większy (np. 24% czy 26%) i całkiem małe na to, że różnica jest duża (np. 20% czy 30%). Proszę zerknąć na wykres (powstał przy założeniu, że liczba zapytanych o poparcie dla partii wynosi n = 600):
Mogę mieć:
- praktycznie pewność (prawdopodobieństwo wynosi 99,6%), że rzeczywiste poparcie mieści się między 20% a 30%,
- duże przekonanie (95% szans), że wynik jest między 21,5% a 28,5%,
- ale już tylko spore szanse (46%), że to jest między 24% a 26%,
- i całkiem małe (22%), że jest to w miarę blisko (24,5%-25,5%) tych sondażowych 25%.
A więc co tak naprawdę znaczy wzrost lub spadek o 1 czy 2 punkty między kolejnymi sondażami? To tylko podniecanie się ułudą, bo jak mawiała Mańka Barcikówna (choć za mądre to dziewczę nie było a i parało się staaaaarym zawodem) od oskomy zęby się psują. Polecam tu przy okazji wpisy PopPolityk, który podaje wartości uśredniane z kilku sondaży, co ma nie tylko ręce i nogi ale również głowę.
Pozostańmy jeszcze na chwilę przy tym „dużym przekonaniu” z 95% szans dla przedziału możliwego wyniki od 21,5% do 28,5% (naukowy termin w statystyce to przedział ufności – niedługo specjalna notka, bo będzie okazja). Granice tego przedziału odległe są od podanej wartości w sondażu o 3,5 punktu (nie punkta!) procentowego. Ta wielkość nosi nazwę maksymalnego błędu szacunku.
Tak! To jest ten mityczny maksymalny błąd podawany (lub często nie) przy wynikach sondaży (nazywany także w mediach błędem badania, błędem oszacowania). I proszę tu zwrócić uwagę na 2 istotne kwestie:
1) nie jest to żaden błąd „maksymalny” w potocznym tego słowa znaczeniu. W znaczeniu statystycznym błąd maksymalny oznacza, że istnieje 95% szans na to, że pomyłka nie będzie większa. A to 95% oznacza, że średnio w co 20(!) oszacowaniu błąd BĘDZIE większy – czysta statystyka;
2) nie jest to też wielkość mitycznych już 3%, którą to z upodobaniem podaje się w mediach, bo w naszym przykładzie nieodległym od rzeczywistości jest to większa wielkość (pochwalę przy okazji HH bo się poprawiło i podaje faktycznie w miarę realny, ale żeby nie było za słodko z jednym ale – patrz dalej).
Wielkość maksymalnego błędu dla próby losowej prostej (i przy niej zostaniemy) wylicza się dość prosto (powiedzmy), wzorek:
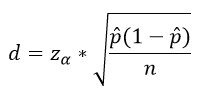
gdzie „z” przyjmuje się, że wynosi 1,96, „p” jest wielkością poparcia dla partii w sondażu zaś „n” liczebnością próby. Czyli np. dla 25% i próby 600 osób obliczenie w Excelu wyglądałoby następująco:
=1,96*PIERWIASTEK(25%*75%/600)
co da nam właśnie wspomniane wyżej 3,5%.
Dlaczego zatem krążą te mityczne 3%. Otóż w sondażu politycznym o głos na partię pyta się tylko osoby, które deklarują pójście na wybory. A to oznacza, że liczebność próby, którą powinno się uwzględniać to nie 1000-1100, gdzie owszem, błąd byłby 3%, a znacznie mniej. W zależności od deklarowanej frekwencji będzie to przeważnie 500-800, a przy wyborach do PE jeszcze mniej.
Warto także wiedzieć, że błąd zależy od wielkości poparcia dla partii (i zaznaczenia tego mi brakuje w przypadku HH). Im poparcie bliższe jest 50% tym błąd (tzw. bezwzględny) jest większy. Na przykład przy próbie pytanych liczącej 500 osób dla partii o poparciu 35% wyniesie 4.2pp podczas gdy dla partii o 10% poparciu będzie to 2,6pp. Inaczej to wygląda jeśli spojrzymy na relację błędu do wysokości poparcia (tzw. względny), przy 35% poparciu błąd 4,2pp to niecałe 12% wyniku a przy 10% 2,6pp to 26%.
I na koniec tabelka z podaną wielkością błędów dla różnych liczebności prób i różnego poparcia.


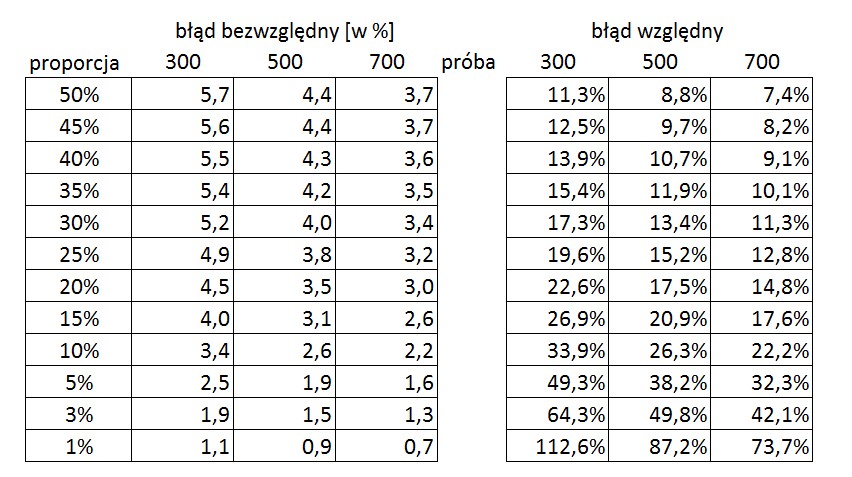




[…] próby a pierwiastek z liczebności próby, napisałem o tym wcześniej w jednej z notek). Ale tu mamy cztery osobne próby, osobno badane na innym kwestionariuszu […]